[ADsP] 3과목

> 1장 데이터 분석 개요

1. 데이터 처리

• 데이터를 분석에 활용하기 위해 데이터웨어하우스와 데이터마트에서 데이터를 가져온다.
• 신규시스템이나 DW에 포함되지 않은 데이터는 기존 운영시스템(Legacy)이나 스테이징 영역(Staging Area)과 ODS(Operational Data Store)에서 데이터를 가져와서 DW에서 가져온 내용과 결합하여 활용할 수 있다.
• 스테이징 영역에서 가져온 데이터는 정제되어 있지 않기 때문에 ODS에서 데이터를 전처리해서 DW나 DM과 결합하여 사용한다.
• ODS는 운영데이터저장소로서 클렌징 영역이며, 기존 운영시스템의 데이터가 정제된 데이터이므로 DW나 DM과 결합하여 분석에 활용할 수 있다.

2. 공간 분석 GIS

• 공간적 차원과 관련된 속성들을 시각화하는 분석
• 지도 위에 관련된 속성들을 생성하고 크기, 모양, 선 굵기 등으로 구분하여 인사이트를 얻음

3. 탐색적 자료 분석 EDA

• 데이터가 가지고 있는 특성을 파악하기 위해 해당 변수의 분포 등을 시각화하여 분석하는 분석 방식
• 데이터 분석에 앞서 전체적으로 데이터의 특징을 파악하고 데이터를 다양한 각도로 접근한다.
• 다양한 차원과 값을 조합해가며 특이한 점이나 의미있는 사실을 도출하고 분석의 최종 목적을 달성해가는 과정
• 데이터를 이해하는 것이 분석 목적
• 데이터에 대한 전반적인 이해를 통해 분석 가능한 데이터인지 확인하는 단계 (데이터이해 단계)
• 데이터에 포함된 변수의 유형이 어떻게 되는지를 찾아가는 과정(변수생성, 변수선택 단계)
• 시각화를 하면 이상점(=이상치, Outlier)을 식별하기 쉽다 ex) R의 Box plot
• 알고리즘 학습: 전적으로 데이터의 품질과 데이터에 담긴 정보량에 달려있다.

1. EDA의 4가지 주제

• 저항성 강조
• 잔차 계산
• 자료변수의 재표현
• 그래프를 통한 현시성

4. 통계 분석

1. 추론 통계

• 모집단으로부터 추출된 표본의 표본통계량으로부터 모집단의 특성인 모수에 관해 통계적으로 추론하는 통계

5. 데이터 마이닝

• 대표적인 고급 분석법으로 대용량의 자료로부터 정보를 요약하고 미래에 대한 예측을 목표로 자료에 존재하는 관계, 패턴, 규칙 등을 탐색하고 이를 모형화함으로써 이전에 알려지지 않은 유용한 지식을 추출하는 분석 방법
• 데이터에 있는 패턴을 파악해 예측하는 분석으로 데이터가 크고 정보가 다양할수록 활용하기 유리한 분석
• 데이터 마이닝 모델링은 통계적 모델링이 아니므로 지나치게 통계적 가설이나 유의성에 집착하지 말아야 한다.
• 분석데이터를 학습 및 테스트 데이터로 상황에 맞게 비율을 나눠 실시한다.
• 성능에 집착하면 분석 모델링의 주목적인 실무 적용에 반하여 시간을 낭비할 수 있으므로 훈련 및 테스트 성능에 큰 편차가 없고 예상 성능을 만족하면 중단한다.

1. 모델링 성능 평가 기준

• 정확도(Accuracy)
• 정밀도(Precision)
• 리프트(Lift)
• 디텍트 레이트(Detect Rate)

> 2장 R프로그래밍 기초

1. 문자형 원소

• 연산할 수 없어서 계산할 시 에러가 뜬다.

2. 벡터

• 하나의 스칼라 값 또는 하나 이상의 스칼라 원소들을 갖는 단순한 형태의 집합이다.
• 한 벡터의 모든 원소는 같은 자료형 또는 같은 모드(mode)를 가진다.
• 위치로 인덱스 된다.
• 벡터는 인덱스를 통해 여러개의 원소로 구성된 하위 벡터를 반환할 수 있다.
• 벡터 원소들은 이름을 가질 수 있다. 
• length가 다른 숫자형 벡터끼리 연산할 경우 에러 메세지와 함께 결과가 출력된다.

3. summary 함수

• 연속형 변수일 경우 4분위수(1st Qu. & 3rd Qu.), 최소값, 최대값, 중앙값, 평균 등을 출력하고 범주형 변수의 경우 각 범주에 대한 빈도수를 출력하여 데이터의 분포를 파악할 수 있게 하는 함수

4. NA

• 결측값을 의미한다.
• NA는 연산 시 NA로 반환한다.
• ==NA로 논리판별을 때리면 결과로 NA를 반환한다.
• NA가 포함된 벡터에 mean 함수를 사용하면 NA가 반환된다.

5. as.numeric 함수

• 자료형 데이터 구조변환에 사용된다.
• FALSE나 TRUE를 숫자형 벡터로 변환한다. (FALSE: 0, TRUE: 1)

6. 데이터프레임 data.frame 함수

• 2차원 목록 데이터 구조에 해당하고, 각 열이 서로 다른 여러가지 데이터 유형을 포함할 수 있다.

7. na.rm=T

• 결측값을 제외

8. plyr 패키지

• 데이터의 분리, 결합 등 필수적인 데이터 처리 기능을 제공한다.
• 데이터 프레임 처리 함수인 ddply 함수를 제공한다.

9. "+"(숫자, 숫자)

• 변수 할당 없이 바로 +를 실행한다.

10. sd 함수

• 데이터프레임에서 선택한 변수의 표준편차를 계산하는 함수
• stdev는 엑셀에서의 함수이다.

11. substr 함수

• (벡터명, n, m)
• 벡터의 요소들에서 n번째부터 m번째까지 글자를 추출할 수 있다.

12. merge 함수

• (데이터프레임1, 데이터프레임2, by=”결합할 기준열의 변수명”)
• 기준열을 기준으로 두 데이터프레임에서 모두 존재하는 행들만으로 결합시킨다.

ex) merge(A, B, by="class")

13. subset 함수

• 조회하고싶은 데이터를 조건에 맞춰서 조회하는 함수

ex) subset(test, 학과==="경영학과")

14. seq 함수

• (n, m, k)
• n부터 m까지 k 간격으로 이루어진 벡터를 반환한다.

15. rbind 함수

• 행으로 결합하는 함수
• 벡터 2개면 1행이 첫번째 벡터, 2행이 두번째 벡터로 결합된다.

16. byrow=T

• 행렬을 생성할 때, byrow=T를 입력하면 데이터가 행을 기준으로 들어간다.

17. 리스트

• R에서 데이터 타입이 같지 않은 객체들을 하나의 객체로 묶어놓을 수 있는 자료구조
• 리스트는 이질적이다.

18. 날짜

• %Y: 네자리 숫자 연도
• %d: 두자리 숫자 일
• %m: 두자리 숫자 월

19. 패키지 설치

• install.packages(”패키지명”) ▶ library(패키지명)

20. sum 함수

• 합을 구하는 함수
• x<-1:100, sum(x>50)의 결과는 50이 나온다.
• x>50은 논리값이기 때문에 이에 해당하는 51, 52, 53 ~ 100까지 TRUE이고 TRUE는 numeric으로 1이다. 그래서 50개이기 때문에 답은 50이다.

21. sqldf

• R에서 SQL의 명령어를 사용 가능하게 해주는 패키지
• SQL을 활용하거나 SAS에서 PROC SQL로 작업하던 사용자들에게 R 프로그램에서 지원해주는 패키지

> 3장 데이터 마트

1. 데이터 마트

• 데이터 웨어하우스(DW)와 사용자 사이의 중간층에 위치한 것으로, 하나의 주제 또는 하나의 부서 중심의 비교적 작은 규모의 데이터 웨어하우스라고 할 수 있다.

2. 파생변수

• 사용자가 특정 조건을 만족하거나 특정 함수에 의해 값을 만들어 의미를 부여한 변수
• 매우 주관적일 수 있으므로 논리적 타당성을 갖추어 개발해야 한다.
• 세분화, 고객행동 예측, 캠페인 반응 예측에 매우 잘 활용된다.
• 대표성이 나타나게 할 필요가 있다.

1. 휴면고객 (휴면가망 변수)

• 많은 기업에서 평균거래주기를 3~4배 이상 초과하거나 다음 달에 거래가 없을 것으로 예상하는 고객

3. reshape 패키지

• 변수를 조합해 변수명을 만들고 시간, 상품 등의 차원에 결합해 다양한 요약변수와 파생변수를 쉽게 생성하여 데이터 마트를 구성할 수 있는 R 패키지

1. melt 함수

• 녹이는 함수
• 데이터셋을 녹인다

ex) MD <- melt(MYDATA, id=c("no", "day")) : 데이터셋을 녹인 후에 no와 day를 기준으로 오름차순 정렬

2. cast 함수

• 녹인 데이터셋을 새로운 구조의 데이터 셋으로 만드는 함수

ex) cast(MD, no+day~variable)

4. plyr 패키지

Multi-Core를 사용하여 반복문을 사용하지 않고도 매우 간단하고 빠르게 처리할 수 있는 데이터 처리 함수를 포함하고 있는 패키지

1. ddply 함수

• 데이터프레임과 summary를 사용하여 새로운 데이터프레임을 반환한다.

ex) ddply(chickwts, ~feed, summarize, groupmean=mean(weight))

5. 결측값(Missing value)

• 결측값 자체가 의미있는 경우도 있다.
• Default 값이 기록된 경우에는 그 값으로 대치한다.
• 결측값이나 이상값을 꼭 제거해야 하는 것은 아니기 때문에 분석의 목적이나 종류에 따라 적절한 판단이 필요하다.
• 결측치가 20% 이상인 경우에는 해당 변수를 제거하고 분석해야 한다.

1. 결측값 처리 방법

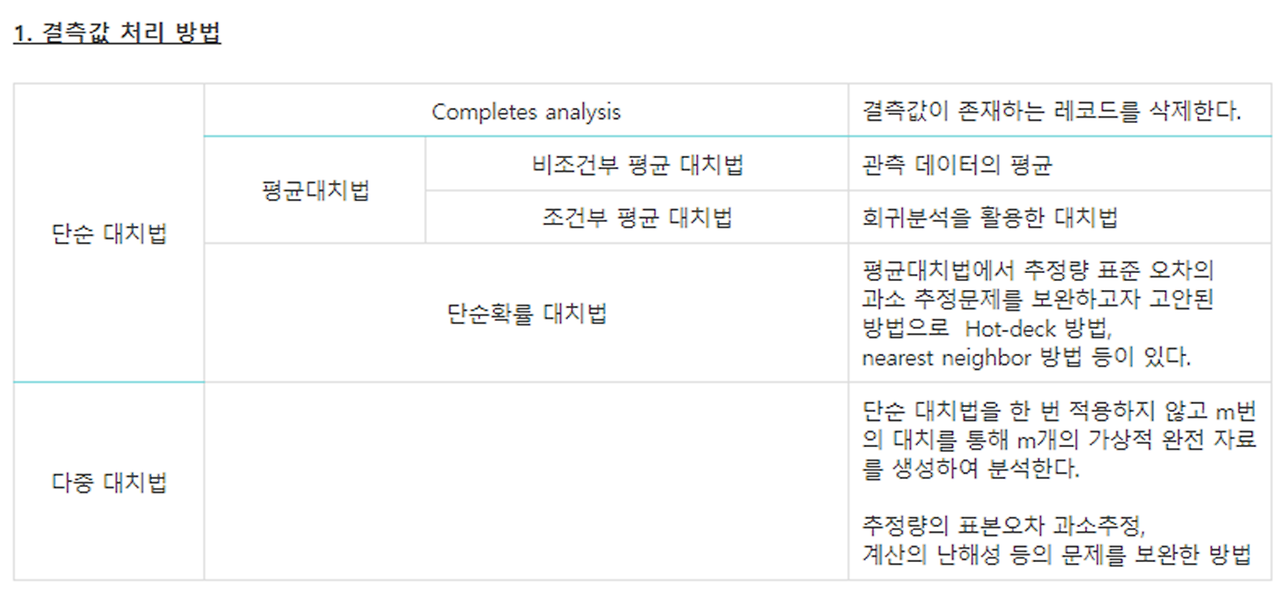
2. R에서 결측값을 처리하는 함수
▷ complete.cases

• 데이터 내 레코드에 결측값이 있으면 FALSE, 없으면 TRUE로 반환한다.

▷ is.na

• 결측값을 NA로 인식하여 결측값이 있으면 TRUE, 없으면 FALSE로 반환한다.

▷ centralImputation

• NA 값에 가운데 값으로 대치, 숫자는 중위수, 요인은 최빈값으로 대치

▷ knnImputation

• NA 값을 k 최근 이웃 분류 알고리즘을 사용하여 대치하는 함수
• k개 주변 이웃까지의 거리를 고려하여 가중 평균한 값을 대치해 주는 함수

▷ rfImpute

• 랜덤 포레스트 모형의 경우, 결측값이 있으면 에러를 발생하기 때문에 랜덤포레스트 패키지에서 NA 결측값을 대치하도록 하는 함수

이상값(Outlier)

• 의도하지 않게 잘못 입력한 경우
• 의도하지 않게 입력되었으나 분석 목적에 부합되지 않아 제거해야하는 경우
• 의도하지 않은 현상이지만 분석에 포함해야 하는 경우
• 의도된 이상값(Fraud, 불량)인 경우
• 이상값을 꼭 제거해야 하는 것은 아니기 때문에 분석의 목적이나 종류에 따라 적절한 판단이 필요하다.
• 데이터 측정과정이나 입력하는 과정에서 잘못 포함됐더라도 삭제하지 않는다.

1. 이상값 인식 방법

1) ESD

• 평균으로부터 3표준편차 떨어진 값

2) 기하평균 - 2.5표준편차 < x < 기하평균 + 2.5표준편차

3) 사분위수 이용하여 제거하기(상자 그림의 outer fence 밖에 있는 값 제거)
: IQR = Q3 - Q1
: Q1 - 1.5IQR < x < Q3 + 1.5IQR ▷ 범위를 벗어나는 x를 제거한다.

2. 이상값 처리 방법

1) 극단값 절단 방법

• 기하평균을 이용한 제거: geo_mean
• 하단, 상단 % 이용한 제거: 10% 절단
• 데이터 손실율이 높아 설명력이 낮아지는 단점이 잇다.

2) 극단값 조정 방법

• 상한값과 하한 값을 벗어난 값들을 하한, 상한값으로 바꾸어 활용하는 방법

3. 이상값 검색을 활용한 응용시스템

• 부정사용방지 시스템

4. 이상값 탐지를 활용한 분야
1) 사기 탐지: 도난 당한 신용카드의 평상시 행위와 다른 구매패턴 조사
2) 의료: 특정 환자에게 보이는 예외적인 증세나 검사 결과는 잠재적 건강 문제
3) 침입탐지: 네트워크에 대한 예외적인 행위를 감시하여 탐지

> 4장 통계 분석

1. 통계 자료의 획득 방법

1. 표본 추출 방법
1) 단순 랜덤 추출법(Simple Random Sampling)

• 각 원소에 임의 번호 부여 후, n개의 번호를 임의 선택 

2) 계통 추출법 (Systemic Sampling)

• 단순 랜덤 추출법의 변형된 방식으로 번호를 부여한 샘플을 나열하여 K개씩 n개의 구간으로 나누고 첫 구간에서 하나를 임의로 선택한 후에 K개씩 띄어서 n개의 표본을 선택하고 매번 K번째 항목을 추출하는 표본 추출 방법

3) 집락추출법(Cluster Random Sampling)

• 군집을 구분하고 군집별로 단순랜덤 추출법을 수행한 후, 모든 자료를 활용하거나 샘플링하는 방법

4) 층화추출법(Stratified Random Sampling)

• 이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 수 있도록 표본을 추출하는 방법으로 유사한 원소끼리 몇 개의 층으로 나누어 각 층에서 랜덤 추출하는 방법이다.
• 서로 유사한 것끼리 몇 개의 층으로 나눈 후 표본을 랜덤하게 추출
• 모집단을 특정한 기준에 따라 서로 상이한 소집단으로 나누고 각각의 소집단으로부터 일정한 표본을 무작위로 추출하는 표본추출방법

2. 측정방법

2. 통계 분석

1. 기술통계

2. 통계적 추론(추측통계)

• 수집된 자료를 이용해 대상 집단에 대한 의사결정을 하는 것으로 Sample을 통해 모집단을 추정하는 것
• 본질적으로 불확실성을 수반한다.

1) 모수추정: 표본 집단으로부터 모집단의 특성인 모수를 분석하여 모집단을 추론한다.
2) 가설검정: 대상 집단에 대해 특정한 가설을 설정한 후에 그 가설이 옳은지 그른지에 대한 채택여부를 결정하는 방법론
3) 예측: 미래의 불확실성을 해결해 효율적인 의사결정을 한다.

3. 확률 및 확률 분포

1. 확률

• 특정 사건이 일어날 가능성의 척도
• 모든 사건 E의 확률값은 0과 1사이에 있다. ▷ 0 <= P(E) <= 1
• 전체 집합 Ω의 확률은 1이다. 즉, P(Ω) = 1
• 서로 배반인 사건들 E1, E2...의 합집합의 확률은 각 사건들의 확률의 합이다.
  (배반사건 = 교집합이 공집합인 사건 ▷ P(A∩B) = ø )
• 두 사건 A, B가 독립이라면 사건 B의 확률은 A가 일어난다는 가정하에서의 B의 조건부 확률과 동일하다.
  두 사건 A, B가 독립이라면 사건 B의 확률 = P(B|A) = P(A∩B) / P(A)

1) 이산형 확률변수 X의 기대값

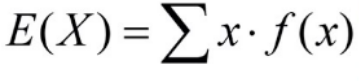
2) 연속형 확률변수 X의 기대값

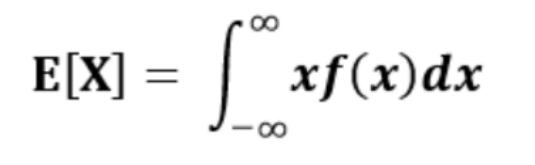
3) 조건부 확률과 독립사건

• 조건부 확률 P(B|A) = P(A ∩ B) / P(A) - P(A) > 0 일 때만 정의된다.
• P(A ∩ B) = P(A) x P(B)이면 , 두 사건이 독립이라는 의미.
• P(B|A) = P(B): 사건 B의 확률은 사건 A가 일어났는지 여부와 무관하다.

2. 이산형 확률변수

1) 베르누이 확률분포
2) 이항분포
3) 기하분포
4) 다항분포

3. 연속형 확률 변수

• 어떤 0보다 큰 값을 갖는 함수의 면적으로 표현, 한 점에서의 확률은 0, 구간에서의 확률값은 확률밀도함수
• 연속형 확률 밀도 함수: 확률변수 X가 구간 또는 구간들의 모임인 숫자 값을 갖는 확률분포함수
• 가능한 값이 실수의 어느 특정 구간 전체에 해당하는 확률변수

1) 균일분포(일양분포)
2) 정규분포
3) 지수분포
4) t-분포
5) 카이제곱분포 (Chi-Square)
6) F-분포

4. 추정과 가설검정

1. 추정

• 표본통계량에 기초하여 모수의 근사값을 결정하는 것
• 표본 평균을 활용해서 모평균을 추정하는 것

1) 점추정(Point Estimation)

• 가장 참값이라고 여겨지는 하나의 모수의 값을 택하는 것
• 표본의 정보로부터 모집단의 모수를 하나의 값으로 추정하는 것
• 표본의 평균, 중위수, 최빈값 등을 사용한다.

2) 구간추정(Interval Estimation)

• 점추정의 정확성을 보완하기 위해 확률로 포현된 믿음의 정도 하에서
  모수가 특정한 구간에 있을 것이라고 선언하는 것이다.
• 항상 추정량의 분포에 대한 전제가 주어져야 하고, 구해진 구간 안에 모수가 있을 가능성의 크기가 주어져야 한다.
• 모수의 참값이 포함되어있으리라고 추정되는 구간을 결정하는 것

3) 신뢰구간

• '신뢰수준 95%'의 의미는 모수가 95%의 신뢰구간 내에 존재할 확률이다.
• 실제 모집단의 모수는 신뢰구간에 포함되지 않을 수 있다.

4) 자유도 df (degree of freedom)

• 통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료 수
• 크기가 n인 표본의 관측값의 자유도는 n-1이다

2. 가설 검정

1) 귀무가설 H0 (Null Hypothesis)

• '비교하는 값과 차이가 없다, 동일하다'를 기본개념으로 하는 가설
• 대립가설과 반대의 증거를 찾기 위해 정한 가설 (보수적으로 지키고자 하는 주장)

2) 대립가설 H1 (Alternative Hypothesis)

• 뚜렷한 증거가 있을 때 주장하는 가설
• 증명하고 싶은 가설 (입증하려는 주장)

3) 검정통계량 (Test Statistic)

• 관찰된 표본으로부터 구하는 통계량
• 검정 시 가설의 진위를 판단하는 기준

4) 유의수준 α (Significance Level)

• 귀무가설이 옳은데도 이를 기각하는 확률의 크기
• 기각역(C)과 동일한 부분

5) 채택역 1 - α (Acceptance Region) 

• 귀무가설을 그대로 채택할 확률의 크기

5. 제1종 오류와 제2종 오류

1. 제1종 오류

• 귀무가설이 사실인데도 불구하고 귀무가설이 사실이 아니라고 판정
• 귀무가설을 기각할 오류

6. 비모수 검정

1. 모수적 방법

2. 비모수적 방법

3. 모수 검정과 비모수 검정의 차이점
1) 모수 검정

• 관측된 자료로 구한 표본평균과 표본분산 등을 이용해 검정을 실시한다.

2) 비모수 검정

• 모집단의 분포에 대해 아무 제약을 가하지 않는다.
• 관측된 자료가 특정 분포를 따른다고 가정할 수 없는 경우에 이용된다.
• 관측된 자료의 수가 많지 않거나 자료가 개체 간의 서열관계를 나타내는 경우에 이용된다.
• 가정된 분포가 없으므로 분포의 형태에 대해 설정한다.
• 관측값들의 절대적인 크기에 의존하지 않고 관측값들의 순위나 두 관측값 사이의 부호 등을 이용해 검증한다.

7. 모분산의 추론

• 표본의 분산은 카이제곱 분포를 따른다.
• 평균모집단(한 집단)에서 n개를 단순임의 추출한 표본의 분산은 자유도가 n-1인 카이제곱 분포를 따른다.
• 모집단의 변동성 또는 퍼짐의 정도에 관심이 있는 경우 모분산이 추론의 대상이 된다.
• 모집단이 정규 분포를 따르지 않더라도 중심극한정리를 통해 정규모집단으로부터 모분산에 대한 검정을 유사하게 시행할 수 있다.
• 이 표본에 의한 분산비 검정은 두 표본의 분산이 동일한지를 비교하는 검정으로 검정통계량은 F-분포를 따른다.

*t- 분포 : 두 집단 간 평균이 동일한 지 확인하기 위해 사용 (자유도 = n - 1)

*F- 분포: 두 집단 간 분산의 동일성 검정에 사용 (자유도 = n - 2)

8. 표본조사

• 응답오차, 유도질문 등은 표본조사에서 유의할 점이다.

1) 표본오차(sampling error)

• 모집단을 대표할 수 있는 표본 단위들이 조사 대상으로 추출되지 못함으로서 발생하는 오차

2) 표본편의(sampling bias)

• 모수를 작게 또는 크게 할 때 추정하는 것과 같이 표본 추출방법에서 기인하는 오차
• 표본추출 과정에서 특정 대상이 다른 대상에 비해 우선적으로 추출될 때 생기는 오차
• 표본 편의는 확률화(randomization)에 의해 최소화하거나 없앨 수 있다. 
• 확률화(randomization): 모집단으로부터 편의되지 않은 표본을 추출하는 절차
• 확률 표본(random sample): 확률화 절차에 의해 추출된 표본 

3) 비표본 오차(non-sampling error)

• 표본오차를 제외한 모든 오차로서 조사과정에서 발생하는 모든 부주의나 실수, 알 수 없는 원인 등 모든 오차
• 조사대상이 증가하면 오차가 커진다.
• 표본값으로 모집단의 모수를 추정할 때 표본오차의 비표본오차가 발생할 수 있다.

9. 기술통계

1. 그래프를 이용한(표본을 도표화함) 모집단 분포 개형
1) 히스토그램

• 연속형으로 표시된 데이터에 표현하며 순서를 바꿀 수 없고 막대의 간격이 없다.
• 도수분포표를 이용하여 표본자료의 분포를 나타낸 그래프
• 수평축 위에 계급구간을 표시하고 각 계급의 상대도수에 비례하는 넓이의 직사각형을 그린 것
• 가로: 계급, 세로: 도수
• 그래프 모양이 치우쳐있거나 봉우리가 여러개 있는 그래프는 비정규 데이터일 수 있다. 그런 경우는 일반적으로 2개 이상의 공정이나 조건에서 데이터가 수집되는 경우 발생한다.

2) 줄기잎그림

• 각 데이터의 점들을 구간단위로 요약하는 방법
• 데이터를 줄기와 잎의 모양으로 그린 그림
• 계산량이 많지 않다.

3) 산점도

• 두 특성의 값이 연속적인 수인 경우, 표본자료를 그래프로 나타내는 방법
• 각 이차원 자료에 대하여 좌표가 (특성 1의 값, 특성 2의 값)인 점을 좌표평면 위에 찍은 것

4) 파레토그림

• 명목형 자료에서 ‘중요한 소수’를 찾는데 유용한 방법

10. 상관분석

1. 상관분석의 유형

2. 피어슨-스피어만 상관계수의 관계

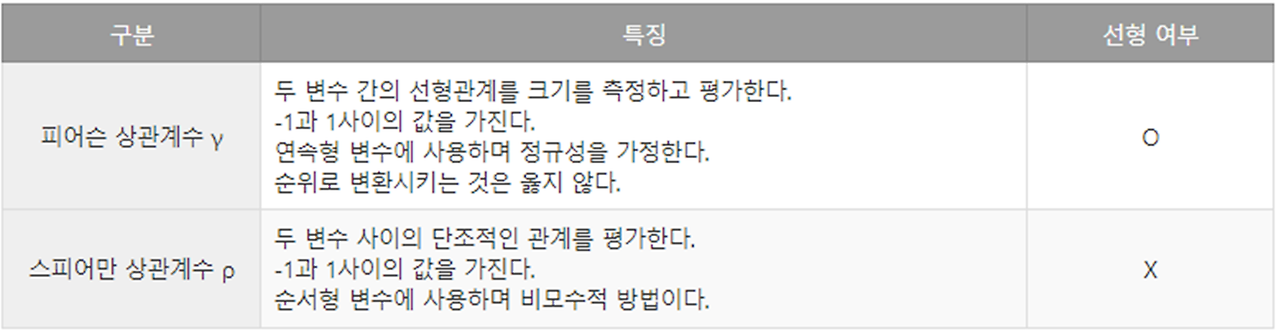
• 상관분석에서는 변수의 분산을 알 수는 없다.

11. 회귀분석

1. 회귀분석의 검정
1) 회귀분석의 가정

• 선형성: 입력변수와 출력변수의 관계가 선형이다.
• 등분산성: 오차의 분산이 입력변수와 무관하게 일정하다.
• 독립성: 입력변수와 오차(잔차)는 관련이 없다.
• 비상관성: 오차(잔차)들끼리 상관이 없다.
• 정상성(정규성): 오차(잔차항)의 분포가 정규분포를 따른다.
• 명목형 변수는 더미변수화하여 사용할 수 있다.

2) 데이터의 정규성을 확인하는 방법

• 히스토그램
• Q-Q plot
• Shapiro-Wilks test

2-1) 데이터의 독립성을 확인하는 방법

• Durbin-Watson test(더빈-왓슨)

2-2) 회귀계수의 추정

• 최소제곱법(최소자승법)

3) 단순 회귀계수의 검정

• 회귀계수인 t-통계량에 대한 p값으로 통계적으로 유의미한지 확인한다.

4) 회귀직선(모형)의 적합도 검토

• 결정계수 R2: 0~1의 값을 가진다. 1에 가까운 값을 가질 수록 추정된 회귀식의 설명력이 높다.
• 결정계수를 통해 추정된 회귀식의 타당성을 검토한다.
• 독립변수가 종속변수 변동의 몇 %를 설명하는지 나타내는 지표이다.
• 다변량 회귀분석(다중 선형회귀분석)에서는 독립변수의 수가 많아지면 결정계수가 높아지므로 독립변수가 유의하지 않아도 변수의 수가 많아지면 결정계수가 높아지는 단점이 존재한다.
• 그래서 다중 회귀분석에서는 최적 모형의 선정기준으로 결정계수 값 보다는 수정된 결정계수 값을 사용하는 것이 좋다.
• 수정된 결정계수는 유의하지 않은 독립변수들이 회귀식에 포함되었을 때 그 값이 감소한다.
• 결정계수 계산법: SSR / (SSE + SSR)
  독립변수 / (Residuals + 독립변수)
• F-통계량으로 확인한다.

2. 다중 선형회귀분석

• 두 개 이상의 독립변수를 사용하여 종속변수의 변화를 설명한다.
• 단순회귀모형이 종속변수의 변동을 설명하는데 충분하지 않다는 점을 보완한 분석 방법
• 모형의 통계적 유의성은 F-통계량으로 확인한다. F-통계량의 p값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다
• 회귀계수의 유의성은 t-통계량으로 확인한다.
• 모형의 적합성은 잔차와 종속변수의 산점도로 확인한다.
• 회귀식에 대한 검정은 독립변수의 기울기가 0이라는 가정을 귀무가설, 기울기가 0이 아니라는 것을 대립가설로 놓는다.

1) 다중공선성

• 독립변수들 간 강한 상관관계가 나타나는 현상
• 모형의 일부 예측변수가 다른 예측변수와 상관되어 있을 때 발생하는 조건이다.
• 중대한 다중공선성은 회귀계수의 분산을 증가시켜 불안정하고 해석하기 어렵게 만들기 때문에 문제가 된다.
• 독립변수의 수가 많아지면 모델의 설명력이 증가하지만 모형이 복잡해지고, 독립변수들 간에 서로 영향을 미친다.
• R에서는 vif 함수를 이용해 VIF값을 구할 수 있으며, 보통 VIF값이 4가 넘으면 다중공선성이 존재한다고 본다.
• VIF는 결정계수에 영향을 받는다. 회귀식의 기울기와는 관계가 없다.

3. Lasso 라쏘 회귀모형

• 가중치 절대값의 합을 최소화하는 것을 제약조건으로 추가하는 기법
• 모형에 포함된 회귀계수들의 절대값의 크기가 클 수록 penalty를 부여한다.
• L1 규제(penalty)를 사용한다.
• 중요하지 않은 가중치는 0이 될 수 있다.
• 자동적으로 변수선택을 하는 효과가 있다.
• Lambda 값으로 penalty의 정도를 조정한다.

12. 최적회귀방정식

1. 설명변수 선택

• 가능한 범위 내에서 적은 수의 설명변수를 포함한다.
• 필요한 변수만 상황에 따라 타협을 통해 선택한다.
• 표준화 자료로 추정한 계수가 가장 큰 변수가 종속변수를 설명하는데 가장 중요하다.

2. 모형선택

• 모든 가능한 독립변수들의 조합에 대한 회귀모형을 고려해 가장 적합한 회귀모형을 선택한다.

3. 단계적 변수선택
1) 전진선택법

• 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가
• 후보가 되는 설명변수 중 가장 설명을 잘하는 변수가 유의하지 않을 때의 모형을 선택한다.
• 설명변수를 추가했을 때 제곱합의 기준으로 가장 설명을 잘하는 변수를 고려하여 그 변수가 유의하면 추가한다.

2) 후진제거법

• 독립변수 후보 모두를 포함한 모형에서 출발해 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 제거할 변수가 없을 때의 모형을 선택한다.

3) 단계선택법

• 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수의 중요도가 약화되면 해당 변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단한다.

4. 영향력 진단

• 적합된 회귀모형의 안정성을 평가하기 위한 통계적 방법

1) 쿡의 거리

• 관측 개체 하나가 제외되었을 때, 최고제곱추정치 벡터의 변화를 표준화한 측도

2) 영향점

• 비교할 대상이 있어 그 값들에 비해 값이 매우 크거나 작아 회귀 계수 추정값을 변화시키는 관측개체를 말한다.

3) DFBETAS

• DFBETAS의 절대값이 유난히 큰 관측개체는 해당 회귀계수의 추정에 대하여 큰 영향력을 행사하는 것으로 간주한다.

4) DFFITS

• DFFITS는 절대값이 공식에 대입한 값보다 큰 값이 나타나야 높은 영향력으로 간주한다.

5. 벌점화 선택기준
1) 설명

• AIC나 BIC의 값이 가장 작은 모형을 선택하는 방법으로 모든 가능한 조합의 회귀분석을 실시한다.
• 모형선택의 일치성
• AIC를 활용하는 방법이 보편화된 방법
• RIC, CIC, DIC 방법도 있다.

6. 모델 성능 평가
1) MAPE

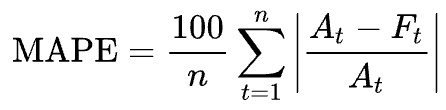
시계열 분석

1. 정의

1) 시계열 자료: 시간의 흐름에 따라 관찰된 값들
2) 시계열 데이터의 분석을 통해 미래의 값을 예측하고 경향, 주기, 계절성 등을 파악하여 활용한다.

2. 시계열 자료의 종류
1) 비정상성 시계열 자료

• 시계열 분석을 실시할 때 다루기 어려운 자료로, 대부분의 시계열 자료가 이에 해당한다.
• 비정상 시계열 자료는 정상성 조건을 만족시켜 정상 시계열로 만든 후 시계열 분석을 한다.

2) 정상성 시계열 자료

• 비정상 시계열을 핸들링해 다루기 쉬운 시계열 자료로 변환한 자료이다.

3. 정상성
1) 평균이 일정할 때

• 모든 시점에 대해 일정한 평균을 가진다.
• 평균이 일정하지 않은 시계열은 차분을 통해 정상화한다.
• 차분: (현 시점 자료 - 전 시점 자료)

2) 분산이 일정할 때

• 분산도 시점에 의존하지 않고 일정해야 한다.
• 분산이 일정하지 않은 시계열은 변환을 통해 정상화한다.

평균차분

분산

변환

3) 공분산도 단지 시차에만 의존할 뿐 특정 시점에 의존하지 않을 때

4) 의미

• 시계열의 수준과 분산에 체계적인 변화가 없고 엄밀하게 주기적 변동이 없다는 것으로 미래는 확률적으로 과거와 동일하다.

4. 시계열 모형(시계열 모델)

1) 자기회귀 모형 AR

• 자기 자신의 과거 값을 사용하여 설명하는 모형
• 백색 잡음(noise)의 현재값과 자기 자신의 과거값의 선형 가중합으로 이루어진 정상 확률 모형
• 모형에 사용하는 시계열 자료의 시점에 따라 1차, 2차, .... p차 등을 사용하나 정상시계열 모형에서는 주로 1, 2차를 사용한다.
• AR(2)는 PACF는 3차항부터 절단 형태, ACF는 지수적 감소를 보인다.

2) 이동평균 모형 MA

• 유한한 개수의 백색잡음의 결합이므로 언제나 정상성을 만족한다.
• MA(2) 였다면 PACF는 지수적 감소, ACF는 3차항부터 절단 형태를 보인다.

3) 자기회귀이동평균 모형 ARMA

• 약한 정상성을 가진 확률 시계열을 표현하는 모형
• ARMA(p, q)로 표기
• ARMA(2, 0)은 AR(2)와 같다.

4) 자기회귀누적이동평균 모형 ARIMA

• 비정상시계열 모형이다.
• 차분이나 변환을 통해 AR모형, MA모형, 이 둘을 합친 ARMA모형으로 정상화 할 수 있다.
• (p, d, q)로 표기한다.
• d=0이면 ARMA(p, q)모형이라 부른다.
• p=0이면 IMA(d, q)모형이라 부르고 d번 차분하면 MA(q)모형을 따른다.
• q=0이면 ARI(p, d)모형이라 부르며, d번 차분한 시계열이 AR(p)모형을 따른다.

5. 분해 시계열

• 시계열에 영향을 주는 일반적인 요인을 분리해 분석하는 방법
• 회귀분석적인 방법을 주로 사용
• 이론적 약점이 있음에도 널리 사용됨

1) 추세변동: 장기적으로 변해가는 큰 흐름. 경제 전반이나 특정 산업의 부침을 나타내 주는 것

2) 계절변동: 요일, 월, 분기 등 고정된 주기에 따른 변화

3) 순환변동: 명백한 이유없이 알려지지 않은 주기를 가지고 변화

4) 불규칙변동: 급격한 환경변화, 천재지변 같은 것으로 발생하는 변동

6. 시계열 데이터의 분석 절차 순서

1) 시간그래프 그리기

2) 추세와 계절성을 제거하기

3) 잔차를 예측하기

4) 잔차에 대한 모델 적합하기

5) 예측된 잔차에 추세와 계절성을 더하여 미래를 예측하기

7. 시계열 데이터

• 시계열 데이터의 모델링은 다른 분석 모형과 같이 탐색 목적과 예측 목적으로 나눌 수 있다.
• 짧은 기간 동안의 주기적인 패턴을 계절변동이라 한다.
• 잡음(noise)은 무작위적인 변동이지만 원인이 알려져있지 않다.
• 시계열분석의 주목적은 외부인자와 관련해 계절적인 패턴, 추세와 같은 요소를 설명할 수 있는 모델을 결정하는 것이다.

13. 다차원척도법 MDS

1. 정의

• 객체간 근접성을 시각화하는 통계기법이다.
• 군집분석과 같이 개체들을 대상으로 변수들을 측정한 후에 개체들 사이의 유사성/비유사성을 측정하여 개체들을 2차원 공간상에 점으로 표현하는 분석방법이다. 
• 여러 대상들 간의 관계를 개체들 사이의 유사성/비유사성을(수치적 자료를 이용해) 상대적 거리로 측정하여 개체들을 2차원 또는 3차원 공간상에 점으로 표현하는(시각화하는) 분석방법이다. 

2. 목적

• 데이터 속에 잠재한 패턴을 찾기 위해 복잡한 구조를 소수 차원의 공간에 기하학적으로 표현하는 것이다.
• 데이터를 고차원에서 저차원으로 축소하는 방법으로 독립변수들간 다중공선성 문제를 해결할 수 있다.

3. 다차원척도법 방법

• 개체들의 거리계산은 유클리드 거리행렬 활용
• 관측대상들의 상대적 거리의 정확도를 높이기 위해 적합 정도를 스트레스 값으로 나타낸다.
• 각 개체들을 공간상에 표현하기 위한 방법은 부적합도 기준으로 STRESS나 S-STRESS를 사용한다.
  

  

4. 다차원척도법 종류
1) 계량적 MDS

• 데이터가 구간척도나 비율척도인 경우 활용한다.

2) 비계량적 MDS

• 데이터가 순서척도인 경우 활용한다.
• 순서척도를 거리의 속성과 같도록 변환하여 거리를 생성한 후 적용한다.

14. 주성분 분석

• 주성분은 주성분을 구성하는 변수들의 계수 구조를 파악하여 적절하게 해석되야 한다. 하지만 명확하게 정의된 해석 방법이 있는 것은 아니다.
• 상관행렬을 사용하여 주성분분석을 시행한다.

1. 주성분 개수(m)를 선택하는 방법

1) 전체 변이 공헌도 방법

• 전체 변이의 70~90% 정도가 되도록 주성분의 수를 결정한다.

2) 평균 고윳값 방법

• 고유값들의 평균을 구한 후 고유값이 평균값 이상이 되는 주성분을 추가하는 방법이다.

3) Scree graph

• 고유값의 크기순으로 산점도를 그린 그래프에서 감소하는 추세가 원만해지는 지점에서 1을 뺀 개수를 주성분의 개수로 선택한다.
  = 고유값이 수평을 유지하기 전 단계로 주성분의 수를 선택한다.
  = 주성분의 개수를 선택하기 위해 총 분산의 비율이 70~90% 사이가 되는 지점을 찾는데 사용되는 그래프

15. 분산분석(ANOVA)

• 두개 이상의 집단에서 그룹 평균 간 차이를 그룹 내 변동에 비교하여 살펴보는 통계 분석 방법
• 두개 이상의 집단들의 평균 간 차이에 대한 통계적 유의성을 검증하는 방법이다.

1. 일원배치 분산분석

• 분산분석에서 반응값에 대한 하나의 범주형 변수의 영향을 알아보기 위해 사용되는 검증 방법이다.
• 모집단의 수에는 제한이 없으며, 각 표본의 수는 같지 않아도 된다.
• F-통계량 (전체 자유도 n - 1, 집단 간 자유도 k - 1, 집단 내 자유도 n - k)
• 잔차(집단 내)의 자유도: n - k
• 회귀(집단 간)의 자유도: k - 1
• n: 표본의 개수
• k: 집단의 수
• 각 집단의 측정치는 서로 독립적이며 정규분포를 따른다.
• 각 집단의 측정치의 분산은 같다. (등분산 가정)
• 결정계수 = SSR / (SSR + SSE) = 집단 간 제곱합 / (집단 간 제곱합 + 집단 내 제곱합)
• 목표변수(종속변수)가 연속형일 때 분류 기준값 선택 방법
  F-통계량, 분산 감소량

16. 교차분석

1. 정의

• 두 문항 모두 범주형 변수일 때 사용하며, 두 변수간 관계를 보기 위해 실시한다.
• 범수의 관찰도수에 비교될 수 있는 기대도수를 계산한다.
• 교차표에서 각 셀의 관찰빈도와 기대빈도 간의 차이를 검정한다.
• 교차표를 작성하여 교차빈도를 집계할 뿐 아니라 두 변수들 간의 독립성 검정을 할 수 있다.
• 기대빈도가 5 미만인 셀의 비율이 20%를 넘으면 카이제곱분포에 근사하지 않으며 이런 경우 표본의 크기를 늘리거나 변수의 수준을 합쳐 셀의 수를 줄이는 방법 등을 사용한다.

2. 카이제곱검정
1) 적합성 검정

• 실험에서 얻어진 관측값들이 예상한 이론과 일치하는지 아닌 지를 검정하는 방법이다.
• 모집단 분포에 대한 가정이 옳게 됐는지를 관측 자료와 비교하여 검정하는 것이다.

2) 독립성 검정

3) 동질성 검정

> 5장 정형 데이터 마이닝

1. 데이터 마이닝

• 대용량 데이터에서 의미있는 패턴을 파악하거나 예측하여 의사결정에 활용하는 방법이다.
• 대용량 데이터 속에서 숨겨진 지식 또는 새로운 규칙을 추출해 내는 과정
• 기업이 보유하고 있는 거래 데이터, 고객 데이터 등과 기타 외부 데이터를 포함하는 모든 데이터를 기반으로 새로운 규칙 등을 발견하고 이를 실제 비즈니스 의사결정 등에 유용한 정보로 활용하고자 하는 일련의 작업

1. 데이터 마이닝의 분석 방법

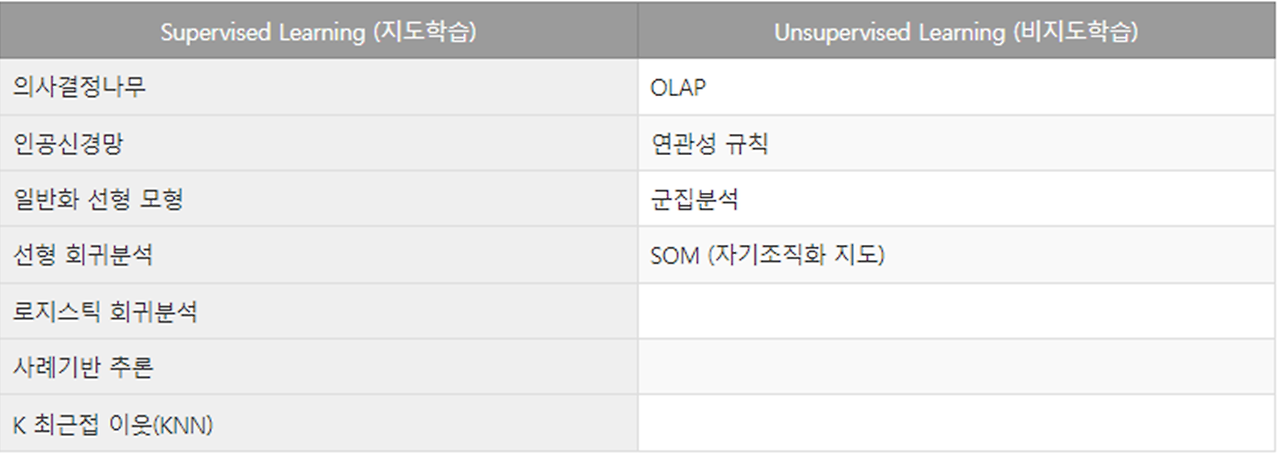
2. 분석 목적에 따른 작업 유형과 기법
1) 분류(Classification)

• 새롭게 나타난 현상을 검토하여 기존의 분류, 정의된 집합에 배정하는 것
• 잘 정의된 분류기준과 선분류되어진 검증 집합이 필요하다.
• 반응변수가 범주형인 경우 예측모형의 주목적이다.
• 의사결정나무, memory-based reasoning, link analysis 등
• R패키지: rpart, rpartOrdinal, party, marginTree, randomForest, tree, MapTree

2) 추정(Estimation)

• '수입, 수준, 신용카드 잔고' 등 연속된 변수의 값을 추정하는 것
• 주어진 데이터를 활용해 알려지지 않은 결과값을 추정한다.
• 신경망 모형

3) 예측(Prediction)

• 분류와 추정과 유사하지만, 미래의 값이라는 차이가 있다.
• 예측 작업의 정확성을 알아보는 방법은 기다리고 지켜보는 것 뿐이다.
• 장바구니 분석, memory-based reasoning, 의사결정나무, 신경망 등이 모두 사용될 수 있다.
• 4) 연관 분석(Association Analysis)
• '같이 팔리는 물건'과 같이 아이템의 연관성을 파악하는 분석
• 장바구니 분석

5) 군집(Clustering)

• 모집단을 동질성을 지닌 그룹으로 세분화하는 것 
• 이질적인 모집단을 세분화하는 기능이 대표적인 기능
• 선분류 되어있는 기준에 의존하지 않는다는 점이 분류와의 차이
• 레코드 자체가 지니고 있는 다른 레코드와의 유사성에 의해 그룹화되고, 이질성에 의해 세분화된다.
• 주로 데이터 마이닝이나 모델링의 준비단계로서 사용된다.

6) 기술(Description)

• 데이터가 가지고 있는 의미를 단순하게 기술하여, 의미를 파악할 수 있도록 한다.
• 데이터가 암시하는 바에 대해 설명이 가능해야 하며, 설명에 대한 답을 찾아낼 수 있어야 한다.
• 사람, 상품에 관한 이해를 증가시키기 위해 데이터의 특징 및 의미를 표현, 설명하는 기능

3. 데이터 마이닝 추진단계

1) 목적 설정

• 데이터 마이닝을 통해 무엇을 왜 하는지 명확한 목적을 설정한다.
• 1단계부터 전문가가 참여하여 목적에 맞는 데이터 마이닝 모델, 기법, 필요 데이터를 정의하는 것이 바람직
• 이해 관계자 모두가 목적에 동의하고 이해할 수 있어야 한다. 

2) 데이터 준비

• IT부서와의 사전 협의, 일정 을 조율하여 데이터 접근 부하에 유의해야 한다.
• 필요시 다른 서버에 저장하여 운영에 지장이 없도록 데이터를 준비한다.
• 데이터 정제를 통해 데이터의 품질을 보장하고, 필요시 데이터를 보강하여 충분한 양의 데이터를 확보한다.

3) 데이터 가공

• 모델링 목적에 따라 목적 변수를 정의한다.
• 필요한 데이터를 데이터 마이닝 소프트웨어에 적용할 수 있는 형식으로 가공한다.

4) 데이터 마이닝 기법 적용

• 1단계에서 명확한 목적에 맞게 데이터 마이닝 기법을 적용하여 정보를 추출한다.

5) 검증

• 데이터 마이닝으로 추출된 정보를 검증한다.
• 테스트 데이터와 과거 데이터를 활용하여 최적의 모델을 선정한다.
• 검증이 완료되면 IT부서와 협의해 상시 데이터 마이닝 결과를 업무에 적용하고 보고서를 작성하여 추가수익과 투자대비성과등으로 기대효과를 전파한다.

4. 데이터 마이닝을 위한 데이터 분할
1) 홀드아웃(Hold-Out) 방법

• 주어진 원천 데이터를 랜덤하게 두 개의 데이터로 구분하여 사용하는 방법으로 주로 학습용과 시험용으로 분리하여 사용한다.
• 무작위로 두 집단으로 분리하여 실험데이터(학습용, 훈련용)와 평가데이터(시험용, 검증용)로 설정하고 검정을 실시하는 모형 평가방법
• 데이터를 학습용 데이터, 검증 데이터, 평가 데이터 세 가지로 분할하여 사용할 수 있다.
  ▷ 검증 데이터 (validation data)
• 학습 중 성능 확인용 데이터 (Overfitting 여부 확인, Early Stopping 등을 위해 사용)

2) k-폴드 교차검증(k-fold Cross Validation)

• 데이터 셋을 K개의 그룹으로 분할한다.
• 주어진 데이터를 k개의 하부집단으로 구분하여 하나의 그룹을 검증용 셋으로, k-1개의 집단을 학습용으로, 나머지는 검증용으로 설정하여 학습한다. k번 반복 측정한 결과를 평균낸 값을 최종값으로 사용한다.
• 모형이 데이터에 과적합하는 문제를 해결하기 위한 방법이다.

5. 성과분석
1) 오분류에 대한 추정치

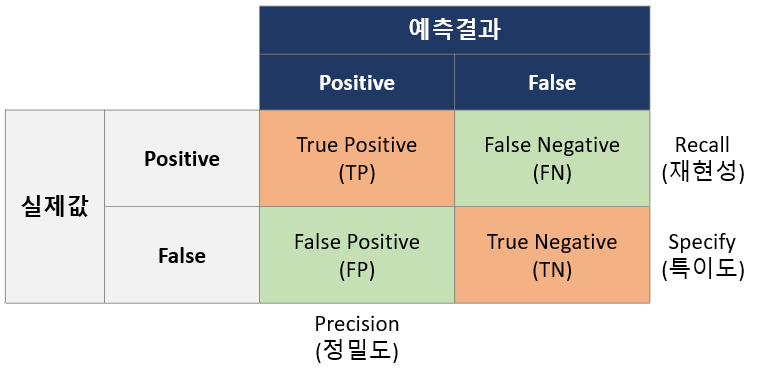
2) ROC Curve

• 모형의 성능을 평가할 때 사용되는 방법론 중 사후확률과 각 분류 기준값에 의해 오분류 행렬을 만든 다음 민감도와 특이도를 산출하여 도표에 도식화하여 평가하는 방식

3) 이익도표
% Captured Response

• 반응검출율 = (해당 등급의 실제 구매자 / 전체 구매자)
• 해당집단에서 목표변수의 특정범주 빈도 / 전체 목표변수의 특정범주 빈도 x 100

5) 향상도 곡선

• 랜덤모델과 비교하여 해당 모델의 성과가 얼마나 향상되었을지를 각 등급별로 파악하는 그래프
• 상위등급에서 매우 크고 하위 등급으로 갈수록 감소하게 되면 일반적으로 모형의 예측력이 적절하다고 판단하게 된다. 

6. 과적합-과대적합, 과소적합

1) 과대적합

• 모형이 학습용 데이터를 과하게 학습하여, 학습 데이터에 대해서는 높은 정확도를 나타내지만 테스트 데이터 혹은 다른 데이터에 적용할 때는 성능이 떨어지는 현상을 의미한다.
• 생성된 모델이 훈련 데이터에 너무 최적화되어 학습하여 테스트 데이터의 작은 변화에 민감하게 반응한다.
• 학습 데이터가 모집단의 특성을 충분히 설명하지 못할 때 자주 발생한다.
• 변수가 너무 많아 모형이 복잡할 때 생긴다. 
• 과대적합이 발생할 것으로 예상되면 학습을 종료하고 업데이트하는 과정을 반복해 과대적합의 방지할 수 있다.

2) 과소적합

2. 분류분석

• 레코드의 특정 속성의 값이 범주형으로 정해져 있으며 데이터의 실체가 어떤 그룹에 속하는지 예측하는데 사용되는 기법으로 사기방지모형, 이탈모형, 고객 세분화 모형 등을 개발할 때 활용한다.
• 고객군을 나눠서 마케팅전략을 수립할 때 적합한 분석 방법

1. 로지스틱 회귀분석

1) 정의

• 독립변수(x)와 종속변수(y) 사이의 관계를 설명하는 모형
• 반응변수(종속변수)가 범주형(y=0 또는 y=1)인 경우에 적용되는 회귀분석모형
• 새로운 설명변수(독립변수)가 주어질 때 반응변수의 각 범주에 속할 확률이 얼마인지를 추정하여 추정확률을 기준치에 따라 분류하는 목적으로 활용한다.
• 클래스가 알려진 데이터의 설명변수들 관점에서 각 클래스 내의 관측치들에 대한 유사성을 찾는데 사용할 수 있다.
• y값의 범위를 [0, 1]로 조정하기 위하여 로짓변환을 사용한다.
• 오즈란 클래스 0에 속할 확률(1-p)이 클래스 1에 속할 확률 p의 비로 나타낸다.
  Odds = p/(1-p)
• 모형 검정 방법으로 카이제곱 검정을 사용한다.

2) 다중로지스틱 회귀모형

• exp( )의 의미는 나머지 변수가 주어질 때 x1이 한 단위 증가 할 때마다 성공(y=1)의 오즈가 몇 배 증가하는지를 나타내는 값이다.

3) 단일 로지스틱 회귀모형 그래프 형태

• 설명변수가 한 개인 경우 회귀계수(β)의 부호에 따라 S자(β>0) 또는 역S자(β<0) 모양을 가진다.

2. 의사결정나무

1) 정의 및 특징

• 분류함수를 의사결정 규칙으로 이뤄진 나무 모양으로 그리는 방법
• 의사결정이 이뤄지는 시점과 성과를 한눈에 볼 수 있게 한다.
• 계산 결과가 의사결정나무에 직접 나타나기 때문에 해석이 간편하다.
• 주어진 입력값에 대하여 출력값을 예측하는 모형으로 분류나무와 회귀나무 모형이 있다.
• 대표적 적용 사례: 대출신용평가, 환자 증상 유추, 채무 불이행 가능성 예측
• 과적합의 문제를 해결하기 위해 가지치기 방법을 이용해 트리를 조정하는 방법을 사용한다.
• 불순도 측도인 엔트로피 개념은 정보이론의 개념을 기반으로 하여, 그 의미는 임의의 사건이 모여있는 집합의 순수성(purity) 또는 단일성(homogeneity) 관점의 특성을 정량화해서 표현한 것이다.
• 가지치기: 과대적합 문제를 방지하는 방법
• 추가로 가지를 생성하면서 단계를 늘리면 새로운 자료에 대한 예측력은 떨어질 수 있다.

2) 학습 방법

• 이익도표 또는 검정용 자료에 의한 교차타당성 등을 이용해 의사결정나무를 평가한다.
• 분리변수의 P차원 공간에 대한 현재 분할은 이전 분할에 영향을 받는다.
• 각 마디에서 최적 분리 규칙은 분리변수의 선택과 분리 기준에 의해 결정된다.
• 가지치기는 분류 오류를 크게 할 위험이 높으나, 부적절한 규칙을 가지고 있는 가지를 제거하는 작업이다.

3) 불순도 측도

• 뿌리마디에서 아래로 내려갈 수록 각 마디에서의 불순도는 점차 감소한다.
  

  

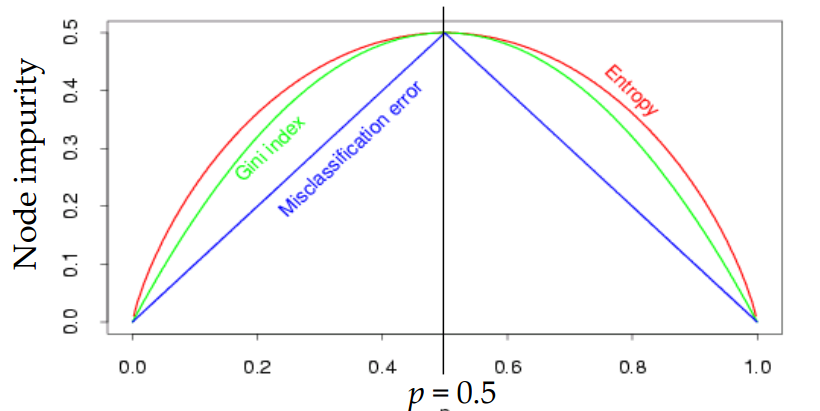
▷ 지니지수

 

▷ 엔트로피 지수: 무질서 정도에 대한 측도

4) 의사결정나무 알고리즘

• CART
• C4.5 / C5.0
• CHAID
• ID3

5) 회귀나무

• 의사결정나무 중 연속형 타깃변수(목표변수, 종속변수)를 예측하는 의사결정나무

3. 나이브 베이즈 분류

• 베이즈 정리와 특징에 대한 조건부 독립을 가설로 하는 알고리즘으로 클래스에 대한 사전 정보와 데이터로부터 추출된 정보를 결합하고 베이즈 정리를 이용하여 어떤 데이터가 특정 클래스에 속하는지를 분류하는 알고리즘

4. K-NN k-최근접 이웃법

• k가 너무 크면 과소적합이 발생하고, k가 너무 작으면 과대적합이 발생할 수 있다.

3. 앙상블 분석

• 주어진 자료로부터 여러 개의 예측모형들을 만든 후 예측모형들을 조합하여 하나의 최종 예측 모형을 만드는 방법
• 종류: 분류기(Classifier) 조합, 다중 모델 조합
• 여러 분류기들의 예측을 조합함으로써 분류 정확성을 향상시키는 기법
• 메타 학습: 다수 모델의 예측을 관리하고 조합하는 기술

1. 앙상블 기법의 종류
1) 배깅

• 원 데이터 집합으로부터 크기가 같은 표본을 여러 번 단순 임의 복원추출하여 각 표본에 대해 분류기를 생성한 후 그 결과를 앙상블하는 방법
• 여러 개의 붓스트랩 자료를 생성하고 각 붓스트랩 자료에 예측모형을 만든 후 결합하여 최종 예측모형을 만드는 방법이다.
• 반복추출 방법을 사용하기 때문에 같은 데이터가 한 표본에 여러 번 추출될 수 있고, 어떤 데이터는 추출되지 않을 수도 있다.

2) 부스팅

• 예측력이 약한 모형들을 결합하여 강한 예측모형을 만드는 방법이다.
• 훈련오차를 빨리 그리고 쉽게 줄일 수 있다.

3) 랜덤 포레스트

• 의사결정나무모형의 특징인 분산이 크다는 점을 고려하여 배깅과 부스팅보다 더 많은 무작위성을 주어 약한 학습기들을 생성한 후 이를 선형 결합해 최종 학습기를 만드는 방법이다.
• 수천 개의 변수를 통해 변수제거 없이 실행되므로 정확도 측면에서 좋은 성과를 보인다.

ex) 자사 고객의 보험갱신 여부를 고객의 인구통계학적 특성, 보험가입 채널, 상품 종류 등의 정보를 사용하여 예측한다.

4) 붓스트랩(Bootstrap)

• 주어진 자료에서 단순랜덤 복원추출 방법을 활용하여 동일한 크기의 표본을 여러개 생성하는 샘플링 방법
• 관측치를 한번 이상 훈련용 자료로 사용하는 복원 추출법에 기반
• 전체 데이터의 양이 크지 않은 경우의 모형 평가에 가장 적합하다.
• 일반적으로 훈련용 자료의 선정을 d번 반복할 때 하나의 관측치가 선정되지 않을 확률이 (1-1/d)^d이다.
• d가 충분히 크다고 가정할 때 훈련용 집합으로 선정되지 않아 검증용 자료로 사용되는 관측치의 비율은 36.8%이다.

ex) 100개의 샘플을 추출하더라도 샘플에 한 번도 선택되지 않는 원데이터가 발생할 수 있다. 그게 36.8%

4. 인공신경망 분석

1. 특징

• 인간 뇌를 기반으로 한 추론 모델
• 일반적으로 인공신경망은 다층 퍼셉트론을 의미한다. 다층 퍼셉트론에서 정보의 흐름은 입력층에서 시작하여 은닉층을 거쳐 출력층으로 진행된다.

1) 신경망 모형

• 동물의 뇌신경계를 모방하여 분류를 위해 만들어진 모형
• 피드 포워드 신경망은 정보가 전방으로 전달되는 것으로 생물학적 신경계에서 나타나는 형태이며 딥러닝에서 가장 핵심적인 구조 개념이다.
• 신경망의 학습 및 기억 특성들은 인간의 학습과 기억 특성을 닮았다.
• 변수의 수가 많거나 입출력 변수 간에 복잡한 비선형관계가 존재할 때 유용하다.
• 잡음에 대해서도 민감하게 반응하지 않는다는 장점을 가지고 있다.

2. 뉴런

• 은닉층의 뉴런 수와 개수는 신경망 모형에서 직접 설정해야 한다.
• 은닉층의 뉴런 수와 개수를 정하는 것은 신경망을 설계하는 사람의 직관과 경험에 의존한다.
• 뉴런 수가 너무 많으면 과적합이 발생하고 뉴런 수가 너무 적으면 입력 데이터를 충분히 표현하지 못하는 경우가 발생한다.
• 뉴런은 활성화 함수를 이용해 출력을 결정하며, 입력신호의 가중치 합을 계산하여 임계값과 비교한다.
  입력변수의 속성에 따라 활성화 함수를 선택하지 않는다. ★
• 뉴런은 기본적인 정보처리 단위
• 뉴런은 가중치가 있는 링크들로 연결
• 뉴런은 여러 입력 신호를 받지만 출력 신호는 오직 하나만 생성
• 입력 링크에서 여러 신호를 받아서 새로운 활성화 수준을 계산하고, 출력 링크로 출력 신호를 보낸다.
• 입력 신호는 미가공 데이터 또는 다른 뉴런의 출력이 될 수 있다.
• 출력 신호는 문제의 최종적인 해(solution)가 되거나 다른 뉴런에 입력될 수 있다.

3. 뉴런의 활성화 함수
1) 시그모이드 함수 Sigmoid

• 입력층이 직접 출력층에 연결되는 단층신경망에서 활성함수를 시그모이드 함수로 사용하면 로지스틱 회귀모형과 작동원리가 유사해진다.
• 로지스틱 회귀분석과 유사하다.
• 0~1의 확률값을 가진다.

2) 소프트맥스 함수 Softmax

• 표준화지수 함수
• 출력값이 여러개로 주어지고 목표치가 다범주인 경우 각 범주에 속할 사후확률을 제공하는 함수 ★
• 출력노드에 주로 사용되는 함수

3) ReLU 함수

• 입력값이 0이하는 0, 0이상은 x값을 가지는 함수
• 최근 딥러닝에서 많이 활용하는 활성화 함수

4. 기울기 소실

• 신경망 모형의 학습을 위한 역전파 과정에서 오차를 더 줄일 수 있는 가중치가 존재함에도 기울기가 0이 되어버려 더 이상 학습이 진행되지 않는 문제를 나타내는 용어

*5. 일반화 가중치8

• 각 공변량들의 효과를 나타내는 것으로 로지스틱 회귀모형에서의 회귀계수와 유사하게 해석된다.

6. 역전파 알고리즘

• 신경망 모형의 목적함수를 최적화하기 위해 사용된다.
• 연결강도를 갱신하기 위해 예측된 결과와 실제값의 차이인 에러(error)의 역전파를 통해 가중치를 조정하는 방법
• 초기값에 따라 결과가 많이 달라지므로 초기값 선택이 매우 중요하다.
• 인공신경망에서 동일 입력층에 대해 원하는 값이 출력되도록 개개의 가중치를 조정하는 방법

5. 군집분석

1. 정의

• 이질적인 모집단을 세분화하는 기능
• 모집단을 동질성을 지닌 그룹으로 세분화하는 것
• 군집에 속한 객체들의 유사성과 서로 다른 군집에 속한 객체간의 상이성을 규명하는 분석 방법
• 군집의 개수나 구조에 대한 가정없이 데이터들 사이의 거리를 기준으로 군집화를 유도한다.

1) 설명

• 군집 결과에 대한 안정성을 검토하는 방법은 교차타당성을 이용하는 방법을 생각할 수 있다.
• 데이터를 두 집단으로 나누어 각 집단에서 군집분석을 한 후 합쳐서 군집분석한 결과와 비교하여 비슷하면 결과에 대한 안정성이 있다고 할 수 있다.
• 군집의 분리가 논리적인가를 살펴보기 위해서는 군집 간 변동의 크기 차이를 검토한다.
• 개체를 분류하기 위한 명확한 기준이 존재하지 않거나 기준이 밝혀지지 않은 상태에서 유용하게 이용할 수 있다.

2-1. 연속형 거리
1) 유클리디안 거리
(x축 차이)^2 + (y축 차이)^2의 제곱근

• 공통으로 점수를 매긴 항목의 크기를 통해 판단하는 측도

2) 맨하탄 거리
x축 차이 + y축 차이 = 직각변 거리

3) 마할라노비스 거리

• 통계적 개념이 포함된 거리이며 변수들의 산포를 고려하여 이를 표준화한 거리
• 변수의 표준화와 변수 간의 상관성을 동시에 고려한 통계적 거리

4) 민코우스키 거리

• 맨하탄거리와 유클리디안 거리를 한번에 표현한 공식으로 L1거리, L2거리라 불리고 있다.

5) 표준화 거리

• 해당변수의 표준편차로 척도 변환한 후 유클리디안 거리를 계산하는 방법
• 척도의 차이, 분산의 차이로 인한 왜곡을 피할 수 있다.

6) 체비셰프 거리

7) 캔버라 거리

2-2. 범주형 거리

1) 자카드 거리

• Boolean 속성으로 이루어진 두 객체 간의 유사도 측정에 사용된다.
• 자카드 계수

2) 코사인 거리

• 두 단위 벡터의 내적을 이용하여, 단위 벡터의 내각의 크기로 유사도를 측정한다.
• 코사인 유사도

3. 계층적 군집분석
1) 정의

• n개의 군집으로 시작해 점차 군집의 개수를 줄여나가는 방법
• 군집의 개수를 미리 정하지 않아도 되어 탐색적 분석에 사용하는 군집 모형
• 덴드로그램: 계층적 군집 분석 결과를 나타내는 도표

2) 연결법
a. 최단연결법(단일연결법 Single linkage method)

• n*n 거리행렬에서 거리가 가장 가까운 데이터를 묶어서 군집을 형성한다.

b. 최장연결법

• 군집과 군집 또는 데이터와의 거리를 계산할 때 최장거리를 거리로 계산하여 거리행렬을 수정하는 방법

c. 평균연결법

• 군집과 군집 또는 데이터와의 거리를 계산할 때 평균을 거리로 계산하여 거리행렬을 수정하는 방법
• 계산량이 불필요하게 많아질 수 있다.

d. 와드연결법

• 병합된 군집의 오차제곱합이 병합 이전 군집의 오차제곱합의 합에 비해 증가한 정도가 작아지는 방향으로 군집을 형성하는 방법

3) Fuzzy Clustering

• 퍼지 이론에 기반하여 관측치가 여러 군집에 동시에 속할 수 있고 각 군집별로 속할 가능성을 제시

4) 밀도기반 군집

• 동일 군집에 속하는 데이터는 서로 근접하게 분포할 것이라는 가정을 기반으로 한 군집분석
• DBSCAN, OPTICS, DENCLUE, STING 등이 있다.

5) 병합적 군집

• 군집을 시작할 때 각 포인트를 하나의 클러스터로 지정하고, 그 다음 종료 조건을 만족할 때 까지 가장 비슷한 두 클러스터를 합친다.

4. 비계층적 군집분석 (k-평균 군집분석, k-Means Clustering)
1) 정의

• n개의 개체를 k개의 군집으로 나눌 수 있는 모든 가능한 방법을 점검해 최적화한 군집을 형성하는 방법
• 주어진 데이터를 k개의 클러스터(군집)로 묶는 알고리즘으로 각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작한다.

2) 특징

• 연속형 변수에 활용이 가능하다.
• k개의 초기 중심값은 임의로 선택이 가능하며 가급적이면 멀리 떨어지는 것이 바람직하다. (군집이 형성되어도 다른 군집으로 이동할 수 있다)
• 초기 중심값의 선정에 따라 결과가 달라질 수 있다.
• 탐욕적 알고리즘이므로 안정된 군집은 보장하나 최적이라는 보장은 없다.

3) 장단점

장점단점

- 알고리즘이 단순하며, 빠르게 수행되어 분석 방법 적용 용이	- 군집의 수, 가중치와 거리 정의가 어렵다
- 계층적 군집분석에 비해 많은 양의 데이터를 다룰 수 있다	- seed값에 따라 결과가 달라질 수 있다(항상 일정한 결과 X)
- 내부 구조에 대한 사전정보가 없어도 의미있는 자료구조를 찾을 수 있다	- 사전에 주어진 목적이 없으므로 결과 해석이 어렵다.
- 다양한 형태의 데이터에 적용 가능	- 잡음이나 이상값의 영향을 많이 받는다.
	- 볼록한 형태가 아닌 (non-convex) 군집이(예를 들어 U형태의 군집) 존재할 경우에는 성능이 떨어진다.
	- 이상값(Outlier)에 민감하여 군집 경계의 설정이 어렵다.
	- 초기 군집수 결정에 어려움이 있다.

• PAM: 이상값에 민감하여 군집 경계의 설정이 어렵다는 단점을 극복하기 위해 등장한 방법. K-Medoid 방법이라고도 하며 평균 대신 중앙값을 이용하여 군집을 선정한다.

4) 과정

• 초기 중심으로부터 오차 제곱합을 최소화하는 방향으로 군집이 형성되므로 집단 내 제곱합 그래프가 필요하다.
• 군집으로 분류된 개체들의 정보를 활용하여 새로운 seed를 계산하면서 개체의 적용에 따른 seed의 변화를 관찰한다.
• 각 데이터를 거리가 가장 가까운 seed가 있는 군집으로 분류한다.
• 원하는 군집의 개수(=k)와 초기값(seed)들을 정해 seed 중심으로 군집을 형성한다.
• 모든 개체가 할당될 때까지 위 과정을 반복해야 한다.

5. 혼합 분포 군집
군집의 크기가 너무 작으면 추정의 정도가 떨어지거나 어려울 수 있다.

1) EM 알고리즘 ★

• k개의 각 혼합모형의 모수와 가중치의 최대가능도 추정에 사용되는 알고리즘

6. SOM(자기조직화 지도)
1) 정의

• 고차원의 데이터를 이해하기 쉬운 저차원의 뉴런으로 정렬화하여 지도의 형태로 형상화하는 클러스터링 방법
• 배깅을 표현한 것
• 비지도 신경망
• 입력층, 경쟁층으로 이루어져 있다.
• BMU: 입력층의 표본 벡터에 가장 가까운 프로토타입 벡터

2) 특징

• 입력변수의 위치 관계를 그대로 보존한다.
• 입력 변수의 정보와 그들의 관계가 지도상에 그대로 나타난다.
• 인공신경망과 달리 단 하나의 전방패스를 사용함으로써 속도가 매우 빠르다.
• SOM 알고리즘은 고차원의 데이터를 저차원의 지도 형태로 형상화하기 때문에 시각적으로 이해하기 쉬울 뿐 아니라 변수의 위치 관계를 그대로 보존하기 때문에 실제 데이터가 유사하면 지도상 가깝게 표현된다.
• SOM은 경쟁 학습으로 각각의 뉴런이 입력 벡터와 얼마나 가까운가를 계산하여 연결강도를 반복적으로 재조정하여 학습한다. 이와 같은 과정을 거치면서 연결강도는 입력 패턴과 가장 유사한 경쟁층 뉴런이 승자가 된다.

7. 최신 군집분석 기법
1) dist( )

• 계층적 군집분석을 위해 거리 계산을 수행하는 함수
• 데이터 행렬의 행 사이의 거리를 계산하기 위해 지정된 거리 측도를 사용하여 계산된 거리 행렬을 계산하고 반환
• 유클리디안, 맥시멈, 맨하탄, 캔버라, 바이너리, 민코우스키

8. 군집모형 평가지표
1) 실루엣

• 한 클러스터 안에서 데이터들이 다른 클러스터와 비교해 얼마나 비슷한가를 나타내는 것, -1과 1사이의 값을 가진다.
• 군집분석의 품질을 정량적으로 평가하는 대표적인 지표로 군집 내의 데이터 응집도와 군집간 분리도를 계산하여 군집 내의 데이터의 거리가 짧을 수록, 군집 간 거리가 멀 수록 값이 커지며 완벽한 분리일 경우 1의 값을 가지는 지표

2) 던 지수

• 군집 간 거리의 최소값(하단 좌측)을 분자, 군집 내 요소 간 거리의 최대값(하단 우측)을 분모로 하는 지표
• 군집 간 거리는 멀수록, 군집 내 분산은 작을 수록 DI(던 지수)가 커진다.

6. 연관분석

조건 반응(if-then)으로 표현되는 연관분석의 결과를 이해하기 쉽다.

1. 연관규칙

2. 기존 이슈

• 대용량 데이터에 대한 연관성분석은 불가능하다.

3. 최근 연관성분석 동향
1) Apriori 알고리즘

• 모든 품목집합에 대한 지지도를 전부 계산하는 것이 아니라, 최소 지지도 이상의 빈발항목집합을 찾은 후 그것들에 대해서만 연관규칙을 계산한다.
• 1세대 알고리즘
• 지지도가 낮은 후보 집합 생성 시 아이템의 개수가 많아지면 계산 복잡도가 증가하는 문제가 있다.
• inspect(): 생성된 연관 규칙을 보기 위해 사용되는 함수

2) FP-Growth 알고리즘

3) 시차연관분석

• 시간이 지남에 따라 어떤 소비형태를 보이는가에 대한 분석으로 원인과 결과의 형태로 해석이 가능해서 결과가 더욱 유용하게 쓰인다.

4) 순차패턴 분석

• 동시에 구매될 가능성이 큰 상품군을 찾아내는 연관성 분석에 시간이라는 개념을 포함시켜 순차적으로 구매 가능성이 큰 상품군으로 찾아내는 데이터마이닝 기법
• 구매시점에 대한 정보가 포함돼있다.

> 6장 비정형 데이터 마이닝

1. 텍스트 마이닝

• 다양한 형태의 문서로부터 텍스트를 획득하여 이를 문서별 단어의 행렬로 만들어 추가적인 분석이나 데이터 마이닝 기법을 적용하여 의사결정을 지원하는 방법
• 자연어처리(NLP) 방식으로 특징 추출, 요약, 분류, 군집화 등 의미를 도출하는 분석이다.

1. 텍스트 마이닝 기능

• 문서 요약(summarization)
• 문서 분류(classification)
• 문서 군집(clustering)
• 특성 추출(feature extraction)

2. 전처리 작업

• 클렌징, 토큰화, 불용어 제거, 어간 추출, 표제어 추출 등

3. 패턴 분석
1) 감정분석

• 문장에서 사용된 긍정단어, 부정단어를 계산하여 해당 문장이 긍정적인지 부정적인지를 평가한다.

2) 워드 클라우드

• 문서에 포함된 단어의 사용 빈도를 효과적으로 보여주기 위해 이용한다.

4. Text To Vector 변환 기법

• 텍스트 데이터 분석을 위해 단어를 벡터화 하는 변환 기법(구조화된 데이터로 변환하는 방법)
• Bag of words, TF-IDF, Word Embedding, Word2Vec 등

5. Corpus(말뭉치)

• 데이터마이닝의 절차 중 데이터의 정제, 통합, 선택, 변환의 과정을 거친 구조화된 단계로 더 이상 추가적인 절차 없이 데이터마이닝 알고리즘 실험에 활용될 수 있는 상태
• 자연언어 연구를 위해 특정한 목적을 가지고 언어의 표본을 추출한 집합

6. TDM, Term Document Matrix

• 문서번호와 단어 간의 사용 여부 또는 빈도수를 이용해 matrix를 만드는 작업

7. Dictionary

• 분석에 사용하고자 하는 단어들의 집합
• 분석하고자 하는 단어들을 별도 사전으로 정의해서 해당 단어들에 대해서만 결과를 산출해보려고 할 때 사용한다.

8. 평가 척도

• 정밀도(Precision) : 모델의 예측값 중 정답과 일치하는 값의 비율
• 재현율(Recall) : 실제 정답 중에서 모델이 정답이라고 예측한 값의 비율

2. 사회연결망분석(SNA)

• 개인과 집단 등의 관계를 노드와 링크로서 모델링하여 그것의 위상구조와 확산 및 진화 과정을 계량적으로 분석하는 방법론

1. 연결망을 표현 하는 분석 방법 종류

• 노드 및 엣지 리스트
• 인접 행렬(Adjacency Matrix)
• 네트워크 그래프(Network Graph)
• 영향력 분석(Influence Analysis)
• 군집화(Clustering) 분석
• 전파(Propagation) 분석

2. 네트워크 표현 방법

• 집합론 : 객체들의 집합에서 각 객체들 간의 관계를 관계쌍(pairs of elements)으로 표현
• 그래프 이론 : 객체를 점(노드), 객체 간의 연결망은 두 점을 연결하는 선(링크)로 표현
• 행렬 : 각 객체를 행렬의 행과 열에 대칭적으로 배치하고, i번째 객체와 j번째 객체가 연결망으로 연결되어 있으면 행렬의 (I, j)번째 칸에 1을 넣고, 연결망이 없으면 0을 넣는다.
• 준연결망(quasi network) : 고객-상품 행렬에서 상품을 구매한 사람들 사이에 직접적인 상호작용의 관계가 없더라도, 관계를 인위적으로 설정해 고객과 고객 또는 상품과 상품 사이의 관계를 나타낸 네트워크

3. 네트워크 구조를 파악하기 위한 기준

• 중심성(Centrality)
• 밀도(Density)
• 구조적 틈새(Structural hole)
• 집중도(Centralization) 등

4. 중심성 분석 지표
1) 중심성(Centraility) : 한 행위자가 전체 연결망에서 중심에 위치하는 정도

• 연결 정도(Degree) 중심성 : 한 점에 직접적으로 연결된 링크의 수
• 근접(Closeness) 중심성 : 한 노드로부터 다른 노드에 도달하기까지 필요한 최소 단계의 합. 각 노드 간 거리를 근거로 중심성을 측정하는 방법
• 매개(Betweenness) 중심성 : 네트워크 내에서 한 점이 담당하는 매개자 혹은 중재자 역할의 정도. 네트워크 간 비교를 위해 사용
• 위세(Eigenvector) 중심성 : 자신의 연결 정도 중심성으로부터 발생하는 영향력과 자신과 연결된 타인의 영향력을 합하여 결정된다. 연결된 노드의 중요성에 가치를 두어 노드의 중심성을 측정하는 방법